I. Introduktion
Vatten kan tända ljus, är det sant? Det är sant!
Är det sant att ormar är rädda för realgar? Det är falskt!
Det vi ska diskutera idag är:
Störningar kan förbättra mätnoggrannheten, är det sant?
Under normala omständigheter är störningar mätningens naturliga fiende. Störningar minskar mätnoggrannheten. I allvarliga fall kommer mätningen inte att utföras normalt. Ur detta perspektiv kan störningar förbättra mätnoggrannheten, vilket är fel!
Men är detta alltid fallet? Finns det en situation där interferens inte minskar mätnoggrannheten, utan istället förbättrar den?
Svaret är ja!
2. Avtal om inblandning
I kombination med den faktiska situationen ingår vi följande överenskommelse om störningen:
- Störningar innehåller inte likströmskomponenter. I den faktiska mätningen är störningarna huvudsakligen växelströmsstörningar, och detta antagande är rimligt.
- Jämfört med den uppmätta likspänningen är interferensamplituden relativt liten. Detta överensstämmer med den faktiska situationen.
- Interferens är en periodisk signal, eller medelvärdet är noll inom en bestämd tidsperiod. Denna punkt är inte nödvändigtvis sann vid faktiska mätningar. Eftersom interferensen generellt är en växelströmssignal med högre frekvens är konventionen om nollmedelvärde rimlig för de flesta interferenser under en längre tidsperiod.
3. Mätnoggrannhet under störningar
De flesta elektriska mätinstrument och mätare använder numera AD-omvandlare, och deras mätnoggrannhet är nära relaterad till AD-omvandlarens upplösning. Generellt sett har AD-omvandlare med högre upplösning högre mätnoggrannhet.
Upplösningen för AD är dock alltid begränsad. Om man antar att upplösningen för AD är 3 bitar och den högsta mätspänningen är 8V, motsvarar AD-omvandlaren en skala uppdelad i 8 divisioner, där varje division är 1V. är 1V. Mätresultatet för denna AD är alltid ett heltal, och decimaldelen antas alltid vara bärbar eller ignorerad, vilket antas vara bärbar i denna artikel. Att bära eller ignorera kommer att orsaka mätfel. Till exempel är 6,3V större än 6V och mindre än 7V. AD-mätresultatet är 7V, och det finns ett fel på 0,7V. Vi kallar detta fel för AD-kvantiseringsfel.
För att underlätta analysen antar vi att skalan (AD-omvandlaren) inte har några andra mätfel förutom AD-kvantiseringsfelet.
Nu använder vi två sådana identiska skalor för att mäta de två likspänningarna som visas i figur 1 utan störningar (idealsituation) och med störningar.
Som visas i figur 1 är den faktiska uppmätta likspänningen 6,3 V, och likspänningen i den vänstra figuren har ingen störning, utan är ett konstant värde. Figuren till höger visar likströmmen som störs av växelströmmen, och det finns en viss fluktuation i värdet. Likspänningen i det högra diagrammet är lika med likspänningen i det vänstra diagrammet efter att störningssignalen eliminerats. Den röda fyrkanten i figuren representerar omvandlingsresultatet från AD-omvandlaren.

Ideal likspänning utan störningar
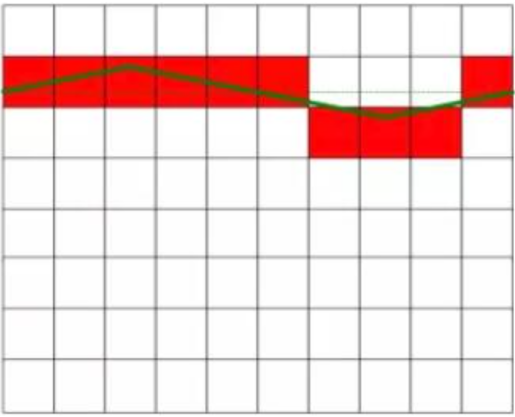
Applicera en störande likspänning med ett medelvärde noll
Gör 10 mätningar av likströmmen i de två fallen i figuren ovan och beräkna sedan medelvärdet av de 10 mätningarna.
Den första skalan till vänster mäts 10 gånger, och avläsningarna är desamma varje gång. På grund av påverkan av AD-kvantiseringsfelet är varje avläsning 7 V. Efter att 10 mätningar har medelvärdesförhållits är resultatet fortfarande 7 V. AD-kvantiseringsfelet är 0,7 V och mätfelet är 0,7 V.
Den andra skalan till höger har förändrats dramatiskt:
På grund av skillnaden i positiv och negativ pol hos interferensspänningen och amplituden, är AD-kvantiseringsfelet olika vid olika mätpunkter. Med förändringen av AD-kvantiseringsfelet ändras AD-mätresultatet mellan 6V och 7V. Sju av mätningarna var 7V, endast tre var 6V, och medelvärdet av de 10 mätningarna var 6,3V! Felet är 0V!
Faktum är att inget fel är omöjligt, för i den objektiva världen finns det inget strikt 6,3V! Det finns dock:
Om det inte finns någon störning, eftersom varje mätresultat är detsamma, förblir felet oförändrat efter att medelvärdet av 10 mätningar beräknats!
När det finns en lämplig mängd interferens, efter att 10 mätningar har medelvärdesbestämts, minskas AD-kvantiseringsfelet med en storleksordning! Upplösningen förbättras med en storleksordning! Mätnoggrannheten förbättras också med en storleksordning!
De viktigaste frågorna är:
Är det samma sak när den uppmätta spänningen har andra värden?
Läsarna kanske vill följa överenskommelsen om interferens i det andra avsnittet, uttrycka interferensen med en serie numeriska värden, lägga interferensen över den uppmätta spänningen och sedan beräkna mätresultaten för varje punkt enligt AD-omvandlarens bärprincip, och sedan beräkna medelvärdet för verifiering, så länge interferensamplituden kan orsaka att avläsningen efter AD-kvantisering ändras, och samplingsfrekvensen är tillräckligt hög (förändringar i interferensamplitud har en övergångsprocess, snarare än två värden positivt och negativt), och noggrannheten måste förbättras!
Det kan bevisas att så länge den uppmätta spänningen inte exakt är ett heltal (den existerar inte i den objektiva världen), kommer det att finnas ett AD-kvantiseringsfel, oavsett hur stort AD-kvantiseringsfelet är. Så länge interferensamplituden är större än AD-kvantiseringsfelet eller större än den minsta upplösningen för AD, kommer det att orsaka att mätresultatet ändras mellan två intilliggande värden. Eftersom interferensen är positiv och negativ symmetrisk är magnituden och sannolikheten för minskning och ökning lika. Därför, när det faktiska värdet är närmare vilket värde, är sannolikheten för vilket värde som kommer att visas större, och det kommer att vara nära vilket värde efter medelvärdesberäkning.
Det vill säga: medelvärdet av flera mätningar (interferensmedelvärdet är noll) måste vara närmare mätresultatet utan interferens, det vill säga att användning av AC-interferenssignalen med ett medelvärde på noll och medelvärdesbildning av flera mätningar kan minska de ekvivalenta AD-kvantiseringsfelen, förbättra AD-mätningsupplösningen och förbättra mätnoggrannheten!
Publiceringstid: 13 juli 2023




